M4208c - Algorithmique avancée
Introduction
Nous avons jusqu’ici rencontré essentiellement deux paradigmes de programmation :
- le paradigme impératif dont les structures de base sont les instructions et les structures de contrôle, paradigme incarné par le langage C ou le langage Lua ;
- le paradigme objet dont les structures de base sont les classes et les messages, paradigme illustré par Java ou C++.
Nous allons dans ce module étudier un troisième paradigme : le paradigme fonctionnel. Celui-ci se caractérise par un certain nombre de particularités (que l’on peut trouver dans les autres paradigmes mais qui sont à leur paroxysme en fonctionnel).
En programmation fonctionnelle, les fonctions sont des citoyens de premier ordre : elles sont traitées de la même façon que les variables. Une fonction est une variable comme les autres, une variable est une fonction comme les autres.
D’autre part, contrairement aux fonctions et surtout au procédures vues en algorithmique, en programmation fonctionnelle, une fonction ne provoque pas d’effets de bord. Cela signifie que le contexte n’agit pas sur la fonction et que celle-ci ne modifie pas les objets. Seuls ses paramètres influent sur le résultat d’une fonction.
Les programmes écrits dans la philosophie fonctionnelle sont très modulaires : composés de nombreuses fonctions très courtes et simples. Un programme est simplement la composition de traitements simples et génériques.
Un des aspects fondamentaux de la programmation fonctionnelle est le recours à la récursivité (voir chapitre 3).
Une fonction associe une valeur à une ou plusieurs valeurs. Elle se définit ainsi qu’en mathématiques non par la suite d’actions à effectuer pour obtenir un résultat mais par l’expression de ce résultat en fonction des entrées.
En java, on écrirait
En un langage fonctionnel, cela deviendra plutôt
poly : x -> (square x) + x + 1Le typage est statique (en Lua ou Python, le typage est dynamique, ce qui signifie que le type d’une variable n’est déterminé qu’à l’exécution) et en général implicite. Il y a donc un mécanisme automatique d’inférence de type.
On dispose de types polymorphes, ce qui permet de réaliser du code générique. Rappelons qu’un type polymorphe peut contenir différents types d’objet ayant des caractéristiques communes (à la manière des interfaces en java ou plus simplement des tableaux qui peuvent être tableaux d’entiers, tableaux de booléens, tableaux de tableaux de réels…).
On dispose enfin d’un mécanisme dit de pattern matching, sorte de switch ... case évolué qui permet de filtrer suivant la forme des entrées d’une fonction.
Fonctions
Une fonction sera définie en associant à ses entrées ses sorties :
somme : x, y -> x+ySi plusieurs cas sont à distinguer, on les énumérera, ainsi que les conditions où ils s’appliquent :
delta : 0 -> 1
n -> 0Ou encore
syracuse : n -> n/2 (si n pair)
n -> 3n+1 (sinon)Ce mécanisme de traitement par cas est nommé pattern matching (filtrage par motif). On remarque qu’à gauche de la flèche, on ne filtre pas sur des expressions complexes mais uniquement sur des valeurs ou des formes (motifs). Pour réaliser un traitement complexe, on ajoute cette condition à la fin.
Les fonctions sont des variables comme les autres, on peut donc écrire des fonctions de fonctions. Par exemple,
adap : f, x -> f(x)+1De même, une fonction peut prendre ses valeur dans l’espace des fonctions. Par exemple, la dérivée pourrait être définie de la façon suivante :
derive : f -> (x -> f'(x))Enfin, les fonctions doivent être typées. Cela signifie que nous devons être capables de dire quels sont les types des entrées et quels sont les types des sorties. Par exemple, la fonction somme prend en entrée deux entiers et donne en sortie un entier. En mathématiques, on dirait f: N² -> N. Nous noterons somme: int * int -> int.
Exercices
Quel est le type de la fonction
integrale?- Définir et donner le type de la fonction de Heaviside (fonction seuil qui vaut 0 sur les nombres négatifs et 1 sur les nombres positifs).
- Définir et donner le type de la fonction de Dirac (fonction qui vaut 1 en 0 et vaut 0 partout ailleurs).
- Définir et donner le type de la fonction créneaux de période 2 valant 1 sur [0,1] et 0 sur [1,2].
Donner le type de la fonction itération qui à f et n associe l’itérée n fois de f :
iteration : f, n -> (x -> f(f(...(f(x))...))- Donner le type de la fonction puissance.
- Définir et donner le type de la fonction composition.
Définir une fonction accroissement qui pour f et δ donne la fonction qui à x associe le taux d’accroissement de f en x sur une largeur δ.
Récursivité
Définitions récursives
récursivité : nom féminin. Caractère de ce qui est récursif.
récursif, ve: adjectif. 1. Qui fait preuve de récursivité. 2. Qui fait appel à lui-même.
Cette définition de récursivité est récursive puisqu’elle fait (indirectement) appel à elle-même. Elle illustre également le danger de la récursivité : la boucle infinie. Cependant, une définition récursive peut être tout à fait correcte et compréhensible : par exemple, cette définition des ascendants généalogiques ne devrait pas poser de problèmes :
ascendant : les ascendants d’une personne sont son père, sa mère et les ascendants de ceux-ci.
La récursivité est présente dans les effets de mise en abîme que l’on peut voir sur les étiquettes de certaines boîtes de fromage.

On remarque que sur l’étiquette, apparaît une boîte de fromage sur l’étiquette de laquelle apparaît une boîte sur laquelle…
La récursivité est également utilisée pour tracer certaines figures fractales comme par exemple le flocon de Koch ou le triangle de Sierpinski.
Il est parfois intéressant de définir une fonction de façon récursive plutôt que de façon itérative. La structure du problème peut s’y prêter (manipulation d’arbres par exemple), la question peut être intrinsèquement récursive (calcul des termes de la suite de Fibonacci par exemple), l’algorithme peut être exprimé de façon beaucoup plus simple sous forme récursive (exemple des tours de Hanoï). Pour illustrer ce point, étudions le casse-tête des tours de Hanoï :
Nous disposons de trois assiettes (une blanche, une bleue et une rouge). Dans l’assiette blanche sont empilées dans l’ordre 7 crêpes de diamètres différents, la plus grande crêpe étant en bas, la plus petite en haut. On souhaite déplacer la pile de crêpes sur l’assiette rouge mais on ne peut déplacer qu’une seule crêpe à la fois et à aucun moment une crêpe ne doit être posée sur une crêpe plus petite. Comment faire ?
Le protocole pour résoudre ce casse-tête est assez simple si l’on suppose que l’on sait déplacer une pile de 6 crêpes en respectant les contraintes : en effet, il suffit de déplacer les 6 crêpes supérieures sur l’assiette bleue, déplacer la dernière crêpe sur l’assiette rouge et enfin déplacer la pile de 6 sur l’assiette rouge. Pour déplacer une pile de 6 crêpes, il va suffire de savoir déplacer une pile de 5, déplacer une crêpe et déplacer la pile de 5. Et ainsi de suite, jusqu’au déplacement d’une pile de 1 crêpe qui ne pose aucun problème.
En termes algorithmiques, on suppose que l’on dispose d’une fonction deplaceCrepe(a1, a2) pour déplacer une unique crêpe de l’assiette a1 à l’assiette a2. Nommons deplacePile(n, assiette1, assiette2) la fonction pour déplacer une pile de n crêpes de l’assiette1 à l’assiette2, il nous suffit de dire :
deplacePile : 1, a1, a2 -> deplaceCrepe(a1, a2)
deplacePile : n+1, a1, a2 -> soit a3 l'assiette qui n'est ni 1 ni 2
deplacePile(n, a1, a3) ;
deplaceCrepe(a1, a2) ;
deplacePile(n, a3, a2)Pour définir la fonction deplacePile, nous avons donc utilisé cette même fonction. Cette fonction est donc récursive. Remarquons que la fonction est bien définie puisque l’appel utilise la fonction sur une pile strictement plus petite et que l’on sait traîter le cas de la pile d’une crêpe.
Considérons maintenant un deuxième exemple : la commande tree. Rappelons que cette commande montre l’arborescence des fichiers et dossiers contenus dans un dossier donné. Par exemple,
% tree .
.
|-- Downloads
| |-- 2259.jpg
| |-- ADECal.ics
| |-- I1-pratique.gnumeric
| |-- I1-théorique.gnumeric
| |-- Philosopher
| | |-- OFL.txt
| | `-- Philosopher.ttf
| |-- Philosopher.zip
| |-- sicp.epub
| `-- zeno.jpg
`-- temp
|-- alire
| |-- Bash-prog.gz
| |-- fourbi
| | |-- 0111118.pdf
| | `-- Zie07.pdf
| |-- Troff
| | |-- cmus.html
| | `-- trofftut.ps
| `-- utp-1.0
| `-- x.ps
|-- cmus1.png
`-- image.JPGSupposons données la fonction liste qui prend en argument un nom de dossier et renvoie un tableau des dossiers contenus ; la fonction estDossier qui prend en argument un nom de dossier et renvoie un booléen. Comment programmer une fonction affichant l’arborescence de dossiers et fichiers de façon similaire à la commande tree ?
La réponse est simple : parcourons la liste du dossier courant. Si nous rencontrons un fichier, nous l’affichons. Si nous rencontrons un dossier, nous l’affichons et faisons son arbre. En d’autres termes, nous pouvons écrire un algorithme ressemblant à ce qui suit (écrit en pseudo-lua)
--- tree affiche l'arborescence des dossiers et fichiers
-- @param dossier la racine a partir de laquelle explorer l'arbre
function tree (dossier)
local lstab, chemin
lstab = liste(dossier)
for i = 1, #lstab do
chemin = lstab[i]
print(chemin)
if estDossier(chemin) then
tree(chemin)
end
end
endOn remarque l’appel récursif à tree(chemin) dans la procédure. Pour éviter de compliquer cette procédure, nous n’avons pas dessiné les branches de l’arbre ni l’indentation de l’arbre. Cela impose en effet de traîter à part le cas du dernier élément du tableau (`-- au lieu de |--) et d’ajouter un paramètre d’indentation à la procédure tree. L’embellissement de cette procédure pour obtenir une fonction complète est laissé en exercice au lecteur. Pour obtenir les fonction liste et estDossier, on pourra ajouter les lignes suivantes au début du fichier lua :
require "lfs"
function liste (d)
local t = {}
for ch in lfs.dir(d) do
if ch ~= ".." and ch ~= "." then table.insert(t, ch) end
end
return t
end
estDossier = function (x) return lfs.attributes(x)["mode"]=="directory" endDe manière générale, on remarque un motif dans les définitions par récurrence de fonctions : on définit tout d’abord un ou plusieurs cas de base où il n’y a pas besoin d’appels récursifs ; on définit ensuite les cas d’héridité (pour reprendre le vocabulaire des preuves par récurrence) c’est-à-dire les cas où pour résoudre le problème, on utilise la solution d’un problème plus simple.
L’exemple de la factorielle est pour celà fort général puisque dans le cas où l’argument est un entier naturel, le cas de base sera le cas où cet argument vaut 1, l’héridité utilisera le cas n-1 pour calculer le cas n.
factorielle : 0 -> 1
n -> n * (factorielle (n-1))Développons le calcul qui est effectué pour calculer 4!.
factorielle 4 = 4 * (factorielle(3))
= 4 * (3 * (factorielle(2)))
= 4 * (3 * (2 * factorielle(1)))
= 4 * (3 * (2 * (1 * factorielle(0))))
= 4 * (3 * (2 * (1 * 1)))
= 4 * (3 * (2 * 1))
= 4 * (3 * 2)
= 4 * 6
= 24Les quatre premières lignes constituent ce que l’on appelle la descente récursive. La cinquième ligne est l’application du cas de base. Les quatre dernières lignes forment la remontée récursive c’est-à-dire les étapes finales de calcul.
Terminaison des fonctions récursives
Au vu de l’exemple de la factorielle, la suite d’appels récursifs se faisant sur des arguments de plus en plus petits, le cas de base va nécessairement être atteint. Néanmoins, la situation n’est pas toujours aussi évidente et il sera alors nécessaire de prouver que la fonction est bien définie, c’est-à-dire que tout calcul entrepris va s’achever. On dira alors que l’on démontre la terminaison de la fonction. Les preuves de terminaison de fonctions récursives vont, du fait de la structure même de la récursion, se faire sous forme de preuve par récurrence. Le cas de base de la preuve correspondant au cas de base de la fonction, la preuve d’hérédité correspondant au cas d’héridité. Certaines fonctions récursives pourront requérir de faire attention à l’hypothèse de récurrence choisie.
Preuve de la terminaison de factorielle
Nommons l’hypothèse “la fonction factorielle termine pour l’entrée n.”.
- Trivialement,
est vraie.
- Supposons
vraie pour un certain n≥0 et montrons que
est alors vraie.
D’après la définition de factorielle, le calcul de factorielle(n+1) nécessite de connaître factorielle(n) (dont le calcul termine par hypothèse), et de multiplier cette valeur par n+1. Donc le calcul de factorielle(n+1) termine.
On en déduit que pour tout n, Hn est vraie.
Exercices
- Définir de façon récursive une fonction
puissance. - Définir récursivement la fonction
fibonacciqui calcule le n-ième terme de la suite de Fibonacci. - Définir de façon récursive la fonction
pgcdqui calcule le plus petit commun diviseur de deux nombres. Indication : supposons a>b, on sait que si p = pgcd(a, b), alors p divise également a-b. - Définir récursivement une fonction
combinaisonscalculant les combinaisons de n éléments parmi p en utilisant les identités connues grace au triangle de Pascal. Définir récursivement la fonction d’Ackermann :
- Calculer à la main la valeur de A(3, 0).
- Un palindrome est un mot qui se lit de la même façon dans les deux sens (par exemple Sennonnes ou 1001). Écrire une fonction récursive testant si un tableau de lettres représente un palindrome.
- Écrire la fonction itération proposée dans les exercices du chapitre 2.
- Prouver la terminaison des fonctions puissance, fibonacci, pgcd et combinaisons.
Considérons la définition de la suite de Syracuse/Collatz :
syracuse : 1 -> 1 n -> n/2 si n pair n -> 3*n+1 si n impairÉcrire une fonction récursive
collatzqui calcule le nombre d’applications de la procédure syracuse pour obtenir 1.Note : la terminaison de cette fonction est un problème ouvert.
Complexité
Nous avons vu en algorithmique que pour résoudre un même problème, différents algorithmes peuvent être écrits. Nous avons constaté que certains algorithmes peuvent être plus efficaces que d’autres (l’énumération des nombres premiers selon la méthode naïve était par exemple impraticable pour de grands nombres alors que l’algorithme du crible d’Erathostène y parvenait). L’efficacité ou la vitesse d’un algorithme peuvent être mesurées par la complexité de cet algorithme.
La complexité en temps d’un algorithme est le nombre d’opérations réalisées par l’algorithme. Ce nombre va s’exprimer en fonction de la taille n des entrées. C’est le comportement de cette complexité quand n tend vers +∞ qui va nous intéresser. Nous parlerons donc de complexité asymptotique. Par exemple, nous dirons d’un algorithme qu’il a une complexité linéaire si le nombre d’opérations réalisées sur une entrée de taille n est de la forme α n + β avec α et β constantes.
Outre la complexité en temps, il existe une notion de complexité en espace. Cette notion mesure la mémoire utilisée par l’algorithme en fonction de la taille de l’entrée. Évidemment, on peut donner une borne de la complexité en espace en fonction de la complexité en temps. Par contre, un algorithme consommant peu de mémoire peut avoir une complexité en temps importante. Nous ne nous attarderons pas sur la complexité en espace même si celle-ci peut être cruciale dans certains cas (c’est la saturation de la mémoire qui va décourager un ordinateur et non le temps de la tâche).
Plusieurs entrées de même taille peuvent produire des temps de calcul fort différents, ainsi la fonction de Collatz définie en exercice au chapitre précédent fait 5 appels récursifs sur l’entrée 32 mais en fait 106 sur l’entrée 31. Nous serons donc intéressés d’une part par la complexité dans le pire des cas (la complexité la plus forte pour toutes les entrées de taille n), dans le meilleur des cas (la plus petite complexité pour toutes les entrées de taille n) et la complexité en moyenne. Il sera évidemment important d’optimiser la complexité en moyenne pour qu’un algorithme se comporte mieux en général et la complexité au pire pour garantir la terminaison de l’algorithme dans tous les cas en temps raisonnable.
Notations de Landau
Pour parler du comportement asymptotique de la complexité, pour comparer le comportement asymptotique de fonctions, nous utiliserons les notations de Landau.
On écrit f = O(g) pour signifier que f est bornée asymptotiquement par g.
On écrit f = o(g) pour signifier que f est dominée asymptotiquement par g.
On écrit f = Θ(g) pour signifier que f et g sont mutuellement bornées l’une par l’autre.
Note : les physiciens utilisent plus volontiers les notations de Hardy (≪). Écrire f ≪ g est équivalent à f = o(g).
Définitions formelles
- f = O(g) ⇔ ∃ k > 0, ∃ u tels que ∀ n > u, |f(n)| ≤ k|g(n)|
- f = o(g) ⇔ ∀ ε > 0, ∃ u tel que ∀ n > u, |f(n)| ≤ ε|g(n)|
- f = Θ(g) ⇔ ∃ λ, μ, u tels que ∀ n>u, λ|g(n)| ≤ f(n) ≤ μ|g(n)|
En termes de limites, on peut écrire
tel que
tel que
Exercices
Soit α et β deux réels strictement positifs.
- Montrer que α n + β = O(n)
- Montrer que α n + β = o(n²)
- Montrer que α n + β = Θ(n)
Démontrer les égalités suivantes :
- O(f) * O(g) = O(f * g)
- Si f=O(g), alors O(f) + O(g) = O(g)
Exemples de classes de complexité
| Symbole | Nom | Complexité |
|---|---|---|
| algorithmes en temps constant | O(1) | |
| LOG | algorithmes en temps logarithmique | O(log n) |
| LIN | algorithmes en temps linéaire | O(n) |
| algorithmes en temps linéarithmique | O(n log n) | |
| P | algorithmes en temps polynomial | |
| EXP | algorithmes en temps exponentiel | |
| Hiérarchie de Grzegorczyk |
En général, on considère que seuls les algorithmes en temps polynomial (ou mieux) sont raisonnables. D’une part ils sont stables par composition (si un algorithme appelle un nombre polynomial de fois un algorithme polynomial, il s’exécute cependant en temps polynomial) contrairement aux classes plus petites. D’autre part, si le temps est asymptotiquement polynomial, cela signifie que le temps de calcul n’augmente pas trop vite quand la taille des entrées augmente contrairement au cas exponentiel. Par exemple, si sur une entrée de taille 10 (par exemple une table d’une base de données à 10 lignes), un algorithme exponentiel met 1 microseconde à répondre, sur une entrée de taille 50, le temps va se compter en dizaines d’années, sur une entrée de taille 100 le temps se comptera en millions de milliards d’années (par comparaison, dans 5 milliards d’années, le Soleil aura englouti la Terre).
Calculs de complexité
Algorithmes itératifs
Dans un algorithme itératif, les instructions prennent un temps de calcul constant, les conditionnelles également. Les boucles par contre vont faire grimper la complexité.
Soit n l’entrée d’un algorithme que nous décomposons dans la suite :
L’instruction dans la boucle est effectuée n fois. La complexité de ce bout de code est donc linéaire en n. En d’autres termes, la complexité est en O(n).
Ici, l’instruction dans la boucle est répétée s fois. Pour savoir la complexité en fonction de n, il faut connaître la valeur de s.
On remarque que s = 1 + 2 + … + n. Il s’agit de la somme d’une suite arithmétique de raison 1. Si on connaît la formule donnant la valeur de cette somme, on peut en déduire que . Si on ne connaît pas la formule, on peut remarquer que s ≤ n + n + … n et donc que s ≤ n². Dans tous les cas, on en déduit que la complexité de cette boucle est en O(n²).
Ici, nous avons deux boucles imbriquées. On constate que pour i fixé, l’instruction print(j) va être appelée i fois. Or, du fait du premier for, i va parcourir l’intervalle [1,n] donc le print va être effectué 1+2+3+…+n fois. De nouveau, on trouve une complexité en O(n²).
Au final, les 3 boucles successives forment un algorithme dont la complexité est en O(n²). En effet, la complexité de la succession de deux éléments est la somme de leurs complexité et O(f) + O(g) = O(g) si f = O(g).
Le cas des itérations non bornées est plus compliqué, en effet, par définition, on ne sait pas à l’avance combien de fois on passera dans le corps de la boucle.
Algorithmes récursifs
Considérons maintenant un algorithme récursif :
factorielle : 0 -> 1
n -> n * factorielle(n-1)Les opérations effectuées sont :
- dans tous les cas, un filtrage pour savoir quel cas appliquer (temps constant),
- dans le cas 0, un résultat immédiat (temps constant),
- dans le cas n, une multiplication, une soustraction et les opérations de factorielle(n-1).
Notons C(n) la complexité de factorielle sur l’entrée n. On a donc et
où
et
sont des constantes (
correspond au temps du filtrage plus celui de la réponse 1 ;
correspond au temps du filtrage plus la multiplication plus la soustraction).
Résolvons cette formule de récurrence pour avoir la complexité asymptotique :
Après addition de toutes les lignes, les C(n-i) s’annulent et on obtient . La complexité de
factorielle est donc linéaire en n.
Master Theorem
Pour introduire l’unique théorème de ce cours, nous allons partir d’un exemple : le produit de matrices.
L’algorithme itératif classique de multiplications de deux matrices n . n a une complexité en O(n³).
L’algorithme récursif naturel va consister, en supposant n pair, à découper chaque matrice en 4 sous-matrices carrées de taille n/2 . n/2, à réaliser les multiplications de ces sous matrices de façon récursive et enfin à compiler les résultats pour calculer la matrice produit. Notons nos matrices de la façon suivante :
On a- R = A.E + B.G
- S = A.F + B.H
- T = C.E + D.G
- U = C.F + D.H.
Notons
le nombre de multiplications nécessaires à la multiplication de deux matrices de taille
. Nous avons
et M(1) = 1. En conséquence, on peut montrer que
La complexité va en fait suivre une loi similaire :
. Le k n² vient du coût des additions : on a 4 additions de matrices de taille n/2 . n/2, ce qui en faisant les additions terme à terme représente n² additions d’entiers. Et on obtient C(n) = O(n³).
- Il existe des algorithmes récursifs plus efficaces : nous allons étudier l’algorithme de Strassen. Introduisons les quantité suivantes :
.
Pour calculer le produit de deux matrices de tailles , on effectue donc 7 multiplications de matrices de taille
. Le nombre de multiplications vérifie donc
où lg est le logarithme en base 2 et lg 7 ≈ 2.8.
La complexité vérifie une loi de la forme . Notons que par cette méthode, le nombre d’additions est plus important donc le k est plus grand que dans le cas précédent. On obtient alors une complexité
. La complexité est donc meilleure que celle de l’algorithme naturel.
Les formules de récurrence obtenues dans les calculs sont assez standard quand on fait du “diviser pour mieux régner”. On voit ainsi apparaître la taille des sous problèmes (ici n/2), le nombre de ces sous-problèmes (ici 7) et le coût de la reconstruction (ici en n²). Mais la résolution de ces équations n’est pas aussi simple que dans le cas de la factorielle. Le Master Theorem donne les équivalent asymptotiques que l’on obtient pour ce genre de formules :
Théorème
Si la complexité C(n) d’un algorithme s’écrit sous la forme
.
On a alors :
- si
, alors
- si
, alors
- si
, alors
.
P = NP ?
Le modèle de calcul classique, les langages de programmation classiques sont déterministes : à une entrée et un contexte donnés correspond une seule exécution.
Il est cependant possible de définir un modèle dans lequel plusieurs exécutions différentes sont possibles. On parle alors de non-déterminisme. Dans un programme non-déterminisme, des choix se font lors de l’exécution du programme. Ces choix peuvent être orientés par une entité extérieure (un oracle) ou être l’occasion pour le programme de se scinder en deux exécutions parallèles.
Par exemple, on appelle NP la classe des problèmes que l’on peut résoudre en temps polynomial par une machine non-déterministe. Plus précisément, un problème est dans NP si étant donnée une instance du problème, on peut vérifier qu’une solution proposée est bien solution en temps polynomial.
Un des problèmes les plus connus appartenant à NP est le problème du voyageur de commerce.
Étant donnés une longueur k, un ensemble de villes et de routes entre ces villes (et donc de distances), existe-t-il un circuit de longueur inférieure à k qui passe par chaque ville une fois et une seule ?
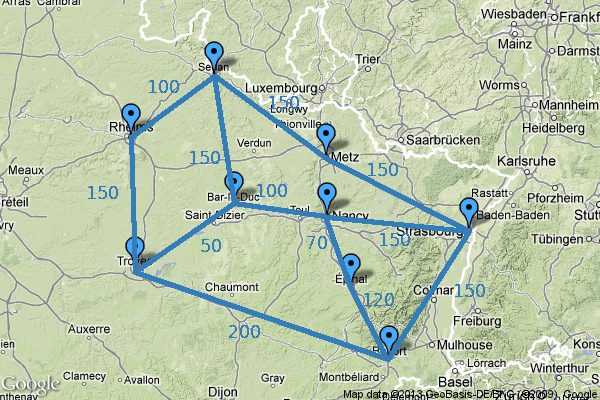
Manifestement, si un problème peut être résolu en temps polynomial (en d’autres termes, s’il appartient à P), il peut être résolu en temps polynomial par une machine non déterministe. Donc P ⊆ NP. Cette inclusion est-elle stricte ? Existe-t-il des problèmes qui peuvent être résolus en temps polynomial par une machine non détermiste mais pas par une machine déterministe ? Cette question est une question ouverte. Il s’agit d’un des 7 problèmes mathématiques sélectionnés par l’Institut de mathématiques Clay dotés d’un prix d’un million de dollars pour celui qui saura le résoudre. Voir http://www.claymath.org/millennium/.
Cette question est importante pour des raisons plus terre à terre. En effet, les algorithmes utilisés en cryptographies pour déchiffrer des messages sont réputés durs et utilisés pour cette raison. Dans la plupart des cas, déchiffrer le message sans la clef est un problème dans NP. Si l’on prouve que P=NP, cela signifiera que le déchiffrement est réalisable en temps polynomial en la taille de la clef, donc relativement facile et toute la cryptographie serait peu fiable.
Notons enfin que le problème du voyageur de commerce est un problème NP-complet. Cela signifie que si l’on sait résoudre ce problème en temps polynomial, tout problème NP peut être résolu en temps polynomial. On peut d’une certaine façon dire que ce problème fait partie des plus difficiles des problèmes NP. De nombreux autres problèmes sont NP-complets.
Exercices
- Montrer que n = o(n log n).
- Montrer que
.
- Montrer que
.
- Écrire un algorithme de recherche d’un élément donné dans un tableau. Calculer la complexité de cet algorithme.
- Écrire un algorithme de recherche d’un élément dans un tableau trié. Calculer la complexité de cet algorithme.
- Calculer la complexité de l’algorithme de puissance proposé précédemment. Chercher un algorithme de calcul de la puissance n-ième ayant une complexité logarithmique en n.
- Écrire un algorithme qui évalue un polynome donné sous la forme d’un tableau de ses coefficients. Calculer sa complexité. Améliorer la complexité en utilisant la méthode de Horner.
- Quelle est la complexité de l’algorithme de calcul du n-ième terme de la suite de Fibonacci. Chercher un algorithme récursif de complexité linéaire en n.
- L’algorithme de plus court chemin de Dijkstra est-il dans NP ? dans P ?
Calculabilité et décidabilité
Thèse de Church-Turing
Les modèles de calcul et les ordinateurs ont été initialement définis pour automatiser des tâches de calcul répétitives faisables par des humains. Un des modèles fondateurs de l’informatique est la machine de Turing (définie par Alan Turing en 1936). Une machine de Turing est composée de 3 éléments fondamentaux :
- la mémoire composée d’un ruban infini ;
- une tête de lecture qui peut écrire ou lire sur le ruban (une seule case à la fois et se déplacer d’une case sur ce ruban ;
- un ensemble fini d’états, dont deux états dit finals qui indiquent si le calcul est terminé ou a échoué.
Le contrôle (la décision d’écrire, déplacer la tête de lecture, changer d’état) se fait en fonction de l’état actuel et du caractère lu par la tête.
Par exemple, la machine définie comme suit calcule la multiplication d’un nombre par 10 :
- On suppose le nombre à multiplier écrit de gauche à droite sur le ruban.
- La tête est sur le premier chiffre (celui de poids fort).
- Si la tête lit un chiffre, la déplacer vers la droite.
- Si la tête lit un blanc, écrire un 0 et passer dans l’état final.
De façon formelle, une machine de Turing est définie par un septuplet : (Q, Σ, Γ, δ, q0, qa, qr).
- Q est l’ensemble des états.
- Σ est l’alphabet d’entrée.
- Γ est l’alphabet de travail (contient au moins Γ et le caractère blanc).
- q0 est l’état initial.
- qa est l’état acceptant.
- qr est l’état rejetant.
On dit qu’un ensemble (de mots ou de nombres) peut être décidé par une machine de Turing s’il existe une machine qui termine sur l’état acceptant quand l’entrée appartient à l’ensemble et termine sur l’état rejetant quand l’entrée n’appartient pas à l’ensemble. On parle alors d’ensemble calculable ou encore récursif (rec)
On dit qu’un ensemble peut être énuméré par machine de Turing s’il existe une machine de Turing qui termine sur l’état acceptant si l’entrée appartient à l’ensemble. On parle alors d’ensemble récursivement énumérable (r.e.).
Note : rec ⊆ r.e.
Théorème (Turing)
La machine de Turing décide les mêmes ensembles que les algorithmes.
On peut donc dire qu’un ensemble est récursif si et seulement s’il existe un algorithme ou un programme dans mon langage de programmation préféré qui répond vrai si l’entrée appartient à l’ensemble et faux sinon. De même, pour récursivement énumérable.
Il existe d’autres modèles de calcul que la machine de Turing, par exemple la machine de Minsky ou les automates cellulaires. Cependant, ces modèles sont aussi puissants que la machine de Turing.
Thèse de Church-Turing
Les algorithmes calculent exactement les mêmes fonctions que tous les modèles de calcul raisonnables.
Puisque tous les modèles de calcul calculent les mêmes fonctions et décident les mêmes ensembles, on peut parler d’ensemble décidable tout court.
Un ensemble X est décidable ssi il est décidable par machine de Turing, ou encore ssi il existe un algorithme f tel que f(x) = vrai si x ∈ X et f(x)=faux sinon.
Nous avons démontré en travaux pratiques d’algorithmique que l’ensemble des nombres premiers est décidable.
Problèmes non calculables ou indécidables
Existe-t-il des problèmes que ne peut pas décider une machine de Turing, existe-t-il des fonctions mathématiques que ne peut calculer un ordinateur ? Oui. L’exemple canonique de problème non décidable est le problème de la halte.
Remarquons que les programmes, les algorithmes sont des objets définis comme une suite de caractères sur un alphabet donné. On peut donc écrire un algorithme sur le ruban d’une machine de Turing. Ainsi, nous pouvons écrire des algorithmes dont les entrées seront des algorithmes. Les compilateurs (javac, gcc) et les interpréteurs (java, lua) sont en pratique des programme prenant un programme comme entrée et en faisant quelque chose. On peut aussi envisager d’écrire des programmes testant si un programme vérifie une propriété (correction syntaxique, bonne indentation ou encore test de bons résultats sur un ensemble de données).
Rappelons qu’il existe des programmes qui ne terminent pas (c’est pour cela que l’on a fait des preuves de terminaison dans un chapitre précédent). Par exemple le programme suivant ne termine que si l’entrée n vaut 0.
Note : en fait en java, ce programme terminera pour de mauvaises raisons : quand n vaudra , n+1 sera négatif (les int vont de
à
).
Peut-on écrire un programme qui étant donné un programme p et une entrée e décide si p termine sur l’entrée e ? Il se trouve que non. La propriété « l’algorithme a termine-t-il sur l’entrée e » est indécidable.
En effet, supposons cette propriété décidable. Appelons halte l’algorithme décidant cette propriété.
Considérons maintenant la machine qui termine sur le programme m si et seulement si m ne termine pas sur l’entrée m. Nous pouvons écrire cette fonction :
Si halte existe, cette fonction v est bien définie. Termine-t-elle sur l’entrée v ?
- Si oui, cela signifie que
halte(v, v)est faux et donc qu’en fait elle ne termine pas. Contradiction. - Si non, cela signifie que
halte(v, v)est vrai et donc qu’en faitv(v)termine. Contradiction.
On ne peut en conclure qu’une chose, la propriété n’est pas décidable.
Théorème
Le problème de la halte («cette machine termine-t-elle ?») est indécidable.
Corollaire
Il existe des problèmes indécidables.
Corollaire (théorème de Rice)
Toute propriété non-triviale sur les programmes est indécidable.
Par exemple :
- Étant donnés deux programmes, savoir s’ils font la même chose est indécidable (on ne peut écrire un programme capable de corriger les devoirs d’algorithmique)
- Il n’existe pas de programme capable de décider si un programme est un virus.
Problème de correspondance de Post
Le problème de la halte est un problème d’autoréférence. Il montre que l’on peut fabriquer des problèmes indécidables mais pas qu’il existe des problèmes indécidables simples. Voyons donc un problème qui semble simple et qui pourtant est indécidable : le problème de correspondance de Post (PCP).
On dispose d’un ensemble donné de dominos différents. Chaque domino comporte sur la case du haut une suite de lettres (éventuellement vide) et sur la case du bas une autre suite de lettres. Chaque domino est disponible en nombre infini. Par exemple,
Peut-on accoler une suite de dominos (non vide) de façon à obtenir la même chaîne en haut et en bas ? Si par exemple on accole le deuxième domino au troisième puis de nouveau au deuxième, on obtient .
Pour cet exemple, la réponse est oui, en effet, en accolant dans l’ordre les dominos 2, 1, 3, 2, 4, on obtient .
Ce problème est indécidable. C’est-à-dire qu’il n’existe pas d’algorithme qui étant donné un jeu de domino saura dans n’importe quel cas dire si oui ou non, il existe une correspondance.
Exercices
- Écrire une machine de Turing qui vérifie que deux mots sont identiques.
- PCP {
,
,
,
}
- Montrer que pour un alphabet unaire (à un seul caractère), PCP est décidable
Introduction à la programmation en caml
Caml est le langage fonctionnel dans lequel nous allons implémenter les algorithmes de ce module.
Lancement d’ocaml
Comme lua (et contrairement à java), ocaml dispose d’un interpréteur dans lequel nous pouvons directement écrire et tester nos programmes.
Sous linux, nous pouvons taper ocaml dans le terminal. Sous Mac OSX, /opt/local/bin/ocaml. Sous windows on utilisera l’environnement ocaml. Note, sous linux et Mac OSX, pour plus de confort (historique des commandes tapées, utilisation des flèches…), nous préfixerons la commande de rlwrap. Nous obtenons un prompt composé d’un # (qu’il ne faudra pas recopier dans les exemples).
ehainry@backus07% rlwrap ocaml
Objective Caml version 3.12.1
# Pour demander l’évaluation d’une entrée, il faut utiliser ;;
# 12;;
- : int = 12
# 12.5
;;
- : float = 12.5
# Ici, les lignes commençant par un - sont les réponses de l’interpréteur. On remarque que celui-ci a typé les nombres que nous lui avons donnés.
Pour travailler, nous écrirons les expressions et fonctions dans un éditeur de texte (gedit, textwrangler, scite…) puis nous copie-collerons dans l’interpréteur. L’extension standard des fichiers caml est .ml.
Constructions de base
Affectations simples de la forme
let identifiant = valeur;;, affectations multiples avecand:# let x = 1;; val x : int = 1 # let y = 1+2 and z = 7+1;; val y : int = 3 val z : int = 8- Opérateurs
- pour les entiers :
+ - * / mod - pour les réels :
+. -. *. /. - pour les booléens :
not and or
# 17 / 3;; - : int = 5 # 17 mod 3;; - : int = 2 # 17. /. 3.;; - : float = 5.66666666666666696 # 17. +. 3;; Error: This expression has type int but an expression was expected of type float # not (true or false);; - : bool = false - pour les entiers :
- Conditionnelles et boucles : il n’y en a pas (pour l’instant). Nous les remplacerons par le filtrage et la récursion.
- Fonctions :
function x -> x+1 ;;affectation d’une fonction :
filtrage :
Dans cet exemple, la valeur denne sert pas, on peut utiliser_qui va accepter n’importe quelle valeur.- appel de la fonction f :
f 12 récursion avec le mot clef
recfonction avec des arguments explicites (éventuellement multiples) :
addest rigoureusement équivalente à :pour filtrer avec des arguments explicites, il faut préciser sur quel argument on filtre (match) :
Évaluation partielle : il est possible de définir une fonction comme l’évaluation d’une autre fonction dont on connaît le ou les premiers arguments :
filtrage sur plusieurs variables :
filtrage conditionnel :
when. Il n’est pas possible de directement filtrer en testant des conditions évoluées, pour cela, on utilise when pour ajouter une condition :
Exercices
- Écrire la fonction qui à un entier associe son carré.
- Écrire la fonction puissance.
- En utilisant puissance, écrire la fonction exponentielle binaire (
)
- Écrire la fonction factorielle.
- Écrire la fonction sommielle.
- Écrire une fonction qui calcule le n-ième terme de la suite de Fibonacci.
- Écrire des fonctions
pairetimpairqui testent si un nombre est pair ou impair. - Écrire une fonction
combinaisonqui calcule les combinaisons de k éléments parmi n en utilisant une identité connue du triangle de Pascal. - Écrire la fonction de Ackermann.
Structures de données récursives
La structure la plus utile quand on programme dans le paradigme impératif est le tableau (éventuellement associatif). Le tableau n’est cependant pas très flexible (suivant les langages, un tableau de tableaux peut n’être possible que si tous les sous-tableaux sont de même taille) et pas du tout adapté à une utilisation récursive. La structure de données récursive canonique est la liste. Nous verrons dans ce chapitre comment utiliser les listes mais aussi comment définir des structures de données récursives et les utiliser dans un langage fonctionnel.
Listes
La liste permet d’arranger des éléments de même type dans une même structure, de façon ordonnée.
La liste est proche de l’ensemble : peut ête vide, peut contenir un ou plusieurs éléments mais contrairement à l’ensemble, les éléments de la liste sont ordonnés et peuvent apparaître plusieurs fois.
Une liste peut être définie de façon récursive comme pouvant être soit vide, soit constituée d’un premier élément (nommé la tête) et d’une liste des éléments suivants (la queue).
En java, la liste serait définie comme une classe dotée de deux attributs : la tête et la queue. On peut penser à une implémentation de la forme suivante pour une liste d’entiers :
La liste vide sera définie par le pointeur NULL (équivalent de nil en lua). La liste [1; 2; 3] sera définie par exemple comme suit :
Notons que dans les langages à pointeurs on nomme la définition équivalente liste chaînée. Il existe également une notion de liste doublement chaînée dans laquelle si une liste est queue de liste, elle comporte un pointeur vers le prédécesseur.
La définition récursive pure est la suivante :
La liste vide
[]est une liste.Si
lest une liste etxun élément alorsx::lest une liste.
On note :: l’opérateur de construction de liste.
Exemple :
Algorithmes sur les listes
Implémenter en caml les fonctions suivantes :
taille ou longueur d’une liste
// taille en Java int taille(Liste l) { int res = 0; while (l != NULL) { l = l.queue; res = res + 1; } return res; }Le filtrage recherche un motif qui pour une liste sera de la forme ou bien la liste vide, ou bien une tête suivie d’une queue. La fonction taille est définie de façon récursive puisqu’on la réappelle sur la queue de la liste.
estVide teste si la liste est vide
estDansteste si un élément donné appartient à la liste.concatenemet deux listes bout à bout.renverserenvoie la liste à l’envers.- Calculer la complexité des fonctions
concateneetrenverse. maximumrenvoie le plus grand élément d’une liste d’entiers.minimumrenvoie le plus grand élément d’une liste d’entiers.repeat n mrenvoie la liste composée denfois l’élémentm.cycle n lrenvoie la liste composée denfois la listel.pairs nrenvoie la liste des n premiers nombres pairs.take n lrenvoie la liste desnpremiers éléments del.drop n lrenvoie la liste des éléments delprivée desnpremiers.lastrenvoie le dernier élément d’une liste.initrenvoie la liste privée de son dernier élément.
Ces fonctions donneront par exemple :
# repeat 5 "ah";;
- : string list = ["ah"; "ah"; "ah"; "ah"; "ah"]
# cycle 4 ["a";"b"];;
- : string list = ["a"; "b"; "a"; "b"; "a"; "b"; "a"; "b"]
# let lp = pairs 10;;
val lp : int list = [2; 4; 6; 8; 10; 12; 14; 16; 18; 20]
# take 4 lp;;
- : int list = [2; 4; 6; 8]
# drop 5 lp;;
- : int list = [12; 14; 16; 18; 20]
# last lp;;
- : int = 20
# init lp;;
- : int list = [2; 4; 6; 8; 10; 12; 14; 16; 18]Piles et files
La pile est une structure de données régie par le principe «Dernier entré, premier sorti» (Last In, First Out ou LIFO en anglais). Elle fonctionne donc comme une pile d’assiette : les nouvelles assiettes sont ajoutées en haut de la pile et quand on a besoin d’une assiette, on la prend en haut de la pile. Comme pour une liste, les éléments sont ordonnés dans la structure, peuvent apparaître de façon multiple et sont rangés linéairement. Cependant, les opérations de base sont légèrement différentes.
Comme pour les listes, une pile peut être vide ou bien constituée d’un sommet posé sur une pile.
On dispose de trois opérations de base pour les piles :
- l’opération
empilerqui ajoute un élément au sommet de la pile, - l’opération
depilerqui supprime le sommet de la pile, - l’opération
sommetqui renvoie le sommet de la pile (sans le dépiler).
Nous allons implémenter un nouveau type en caml :
On dit qu’une pile d’alpha (par exemple une pile d’entiers) est soit la pile vide, soit E(x, p) ou x est un alpha et p une pile d’alpha.
let empiler x p = E(x, p);;
let depiler = function E(x, p) -> p;;
let sommet = function E(x, p) -> x;;Remarquons que les fonctions depiler et sommet ne traitent pas le cas de la pile vide, il faudra donc faire attention à ne les utiliser que sur des piles non vides.
La file (ou queue) est une structure de données régie par le principe «Premier entré, permier sorti» (First In , First Out ou FIFO en anglais). Elle fonctionne comme une file d’attente : les nouveaux clients sont ajoutés au bout de la queue, il faut être en tête de queue pour accéder au guichet.
Exercices
- Écrire une fonction calculant la hauteur d’une pile.
- Implémenter le type file et les opérations de base :
enfiler,defilerettete. La pile est utile pour parcourir des données sous forme arborescente, par exemple les expressions arithmétiques. Par exemple, supposons que l’on dispose d’une expression bien parenthésée, si on parcourt l’expression, en empilant quand on rencontre une parenthèse ouvrante et dépilant quand on rencontre une parenthèse fermante, à la fin, la pile sera vide et à aucun moment, on aura essayé de dépiler une pile vide.
Écrire une fonction qui étant donnée une liste de 0 et de 1 (représentant respectivement les parenthèses ouvrantes et fermantes) dit si l’expression est bien parenthésée.
Arbres
En mathématiques, on définit un arbre comme un graphe non orienté connexe et acyclique. Un graphe étant un ensemble de nœuds, et de liens nommés arêtes joignant certaines paires de nœuds. La connexité signifie que d’un nœud donné, on peut atteindre n’importe lequel des autres nœuds en suivant des arêtes. L’acyclicité indique l’absence de cycle, c’est-à-dire de chemin formant une boucle.
Plus simplement, un arbre est un ensemble de nœuds (ou sommets) qui peuvent être connectés les uns aux autres sans former de boucle.
Un arbre est dit enraciné si on distingue un sommet particulier appelé racine. On ne considèrera dans la suite que des arbres enracinés.
Par exemple, les trois arbres suivants ne sont différents que si on les considère enracinés (le sommet bleu est considéré comme racine sur les deux premiers arbres) :
La racine impose de fait un sens de parcours de l’arbre. L’orientation dépend donc de l’utilisation qu’on veut faire de l’arbre. Par exemple, en bio-informatique, on réalise des arbres phylogénétiques montrant les relations de parenté entre espèces par rapport à leur matériel génétique. Le choix d’une racine peut grandement modifier l’interprétation que l’on fait de l’arbre.
Quand deux nœuds sont liés, le plus proche de la racine est appelé père et l’autre est le nœud fils.
Propriétés et définitions
- Deux nœuds quelconques d’un arbre sont liés par un unique chemin élémentaire.
- La racine est le seul nœud qui n’a pas de père.
- Un nœud sans fils est appelé feuille.
- Un nœud qui n’est pas une feuille est appelé nœud interne.
- Le degré d’un nœud est le nombre de fils de ce nœud.
- La profondeur d’un nœud est la longueur du chemin entre la racine et ce nœud. La racine a profondeur 0, ses fils ont profondeur 1…
- Le degré d’un arbre est le degré maximal des nœuds. Dans les arbres de l’exemple, le premier est de degré 3, le deuxième de degré 2.
- La hauteur d’un arbre est le maximum des profondeurs des nœuds.
Représentation des arbres
Pour représenter un arbre, on peut utiliser une structure contenant une valeur, un pointeur vers chacun des fils et éventuellement un pointeur vers le père. Ce qui en java donnerait une classe de la forme :
Cela implique de connaître le degré de l’arbre avant de définir la structure de données. Plutôt que des pointeurs vers chacun des fils, on peut penser à définir un arbre à l’aide de son premier fils et son frère cadet.
Cette structure correspond à utiliser une liste chaînée pour représenter les fils. Il peut être plus naturel en java d’utiliser un tableau des fils.
En caml, c’est la solution de la liste de fils que l’on retiendra. De façon récursive, un arbre est soit l’arbre vide noté Λ (Lambda), soit un nœud comportant une valeur et une liste de fils (éventuellement vide) :
type 'a arbre = ALambda | Noeud of 'a * 'a arbre list;;
let bonsai = Noeud(7, [Noeud(3, []); Noeud(9, [Noeud(1, [])]); Noeud(4, [])]);;
val bonsai : int arbre =
Noeud (7, [Noeud (3, []); Noeud (9, [Noeud (1, [])]); Noeud (4, [])])L’arbre bonsai correspond au premier arbre dessiné dans l’exemple ci-dessus.
Arbres binaires
Un arbre binaire est un arbre ordonné de degré 2 dans lequel le fait d’être fils gauche ou fils droit a une importance.
Un arbre binaire peut être filiforme (tous les nœuds internes sont de degré 1), localement complet (tous les nœuds internes sont de degré 2) ou complets (parfois appelés parfaits) (localement complet et toutes les feuilles sont à même profondeur.
Comme nous connaissons le nombre de fils dans un arbre binaire, on peut éviter d’utiliser une liste et dire qu’un arbre binaire est soit l’arbre binaire vide Λ, soit un nœud constitué d’une valeur, un sous arbre gauche et un sous arbre droit noté 〈G, v, D〉 où G et D sont les sous arbres gauche et droit.
Ainsi, le deuxième arbre de l’exemple (qui est binaire) peut être noté :
que l’on racourcit parfois en enlevant les sous arbres des feuilles :
En caml, on utilisera le type suivant ;
type 'a tree = Lambda | Node of 'a tree * 'a * 'a tree;;
let exampletree = Node(Lambda, 7, Node(Lambda, 2, Lambda));;Parcours d’un arbre binaire
Nous considérerons l’arbre suivant comme exemple :
- Parcours en profondeur
Parcours préfixe
Le parcours préfixe consiste à afficher la racine, puis à explorer (par parcours préfixe) le sous arbre gauche, puis à explorer le sous arbre droit.
Sur l’exemple, on obtient* - 1 + 8 2.Parcours infixe
Le parcours infixe consiste à explorer d’abord le sous arbre gauche, puis à afficher la racine, puis à explorer le sous arbre droit. Si l’arbre représente une expression arithmétique, ce parcours donne l’expression sous la forme classique.
Sur l’exemple, on obtient- 1 * 8 + 2(il ne manque que les parenthèses).Parcours postfixe
Le parcours postfixe consiste à explorer à gauche, puis à droite puis à afficher la racine. Pour un arbre représentant une expression arithmétique, ce parcours donne sa version en RPN (Reverse Polish Notation) c’est-à-dire la version que l’on peut faire évaluer par une calculatrice à pile (les mêmes que dans la partie piles et files).
Sur l’exemple, on obtient
1 - 8 2 + *. Si en parcourant ces valeurs on empile les nombres et que quand on rencontre un opérateur, on dépile autant d’opérandes qu’il faut puis on empile le résultat de l’opération, on obtient à la fin la valeur de l’expression (notons que le - pouvant être unaire ou binaire, il peut y avoir des problèmes).
Parcours en largeur
Le parcours en largeur est plus simple à visualiser mais plus difficile à implémenter que les parcours en profondeur (avec notre structure récursive). Il consiste à afficher les nœuds rencontrés sur la première ligne (la racine), puis les nœuds rencontrés sur la deuxième ligne de gauche à droite, puis les nœuds rencontrés sur la ligne suivante de gauche à droite, jusqu’à avoir exploré tous les nœuds. Sur l’exemple ci-dessus, on obtient
* - + 1 8 2
Algorithmes sur les arbres binaires
- Écrire des algorithmes récursifs pour chacune des fonctions suivantes :
- taille d’un arbre binaire (la taille est le nombre de nœuds)
- hauteur d’un arbre binaire
- estDans : recherche d’une valeur dans un arbre binaire (quelconque).
- Calculer la complexité de ces algorithmes.
- Montrer que dans un arbre binaire, si on appelle t la taille et h la hauteur, on a
Nous disposons d’un arbre binaire représentant une expression arithmétique. Les nœuds contiennent des éléments appartenant au type noeud défini ci-après. Implémenter une fonction évaluant l’expression en question à l’aide d’un parcours postfixe (pour obtenir l’expression en RPN) et utilisant une pile pour faire les calcules.
Arbres binaires de recherche
Les arbres binaires de recherche (abr) vont être utiles pour ordonner des éléments et optimiser la recherche d’un élément dans l’arbre. On a vu précédemment que la recherche dans un arbre binaire quelconque implique d’explorer chacun des sous arbres. Si on impose que tous les éléments du sous arbre gauche sont inférieur à la racine et tous les éléments du sous arbre droit sont supérieurs à la racine, on n’a plus à explorer un des sous arbres pour trouver un élément.
A est un abr si l’une des conditions suivantes est vraie :
- A = Λ
- A = 〈G, r, D〉 et G et D sont des abr et ∀x∈G, x≤r et ∀x∈D, x≥r.
Exemples
Deux exemples d’abr :
6
6 /
/ \ /
/ \ 5
4 8 /
/ \ / \ /
1 5 7 9 4Un exemple d’arbre binaire qui n’est pas un abr :
6
/ \
/ \
5 9
/ \
/ \
3 4Exercices
- Écrire un algorithme testant si un arbre binaire est un abr.
- Écrire un algorithme de recherche dans un abr.
- Calculer la complexité de cet algorithme de recherche dans le meilleur des cas (arbre parfait).
- Écrire un algorithme d’insertion dans un abr (préservant l’abr-ité).
Algorithmes de tri
Tri bulle
Dans le module d’algorithmique, nous avons vu un algorithme de tri d’un tableau. Il consistait à parcourir le tableau en inversant les éléments si on rencontrait un indice i du tableau tel que t[i] > t[i+1]. L’algorithme s’arrêtait quand le tableau était entièrement trié. Cet algorithme est appelé tri bulle.
function tri (t)
esttrie = false
longueur = #t
while not esttrie do
esttrie = true
for i = 1, longueur-1 do
if t[i] > t[i+1] then
esttrie = false
t[i], t[i+1] = t[i+1], t[i]
end
end
end
return t
endDu fait de la boucle while, il n’est de calculer la complexité de cet algorithme. Nommons n la longueur du tableau. On remarque qu’à chaque passage dans la boucle while, on parcourt tout le tableau par une boucle for. Cette boucle for a donc une complexité en O(n). On peut se convaincre que l’algorithme termine puisque à chaque itération, le tableau est de mieux en mieux trié (l’inversion supprime un obstacle au tri). On peut aussi se convaincre qu’au bout de n passages dans la boucle while, le tableau sera trié, en effet, après le premier passage, le dernier élément du tableau est nécessairement remonté tout à la fin (comme les bulles dans une boisson gazeuse), après le deuxième passage, les deux derniers éléments du tableau seront les deux plus grands (dans l’ordre), … et après n passages, les n éléments sont dans l’ordre. La complexité au pire est donc en O(n²).
Nous allons maintenant chercher des algorithmes de tri récursifs et de préférence plus efficaces que le tri bulle. Au lieu d’un tableau, nous allons supposer que les éléments sont dans une liste (plus adaptée aux algorithmes récursifs).
Pour une visualisation de chacun de ces algorithmes (y compris le tri-bulle ci-dessus) on pourra étudier les vidéos sur http://www.youtube.com/user/AlgoRythmics/videos. En anglais, le tri bulle est appelé bubble sort, le tri pivot est appelé quick-sort, le tri fusion est appelé merge-sort.
## Tri insertion
Étant donnée une liste, soit elle est vide (auquel cas elle est déjà triée). Soit elle est composée d’une tête et d’une queue. Si je suppose la queue triée, il ne reste plus qu’à insérer la tête au bon endroit. Nous allons donc écrire une fonction d’insertion dans une liste triée et la fonction tri_insertion qui réalise le tri :
let rec insertion x liste = match liste with
| [] -> [x]
| t::q -> if t>x
then x::liste
else t::(insertion x q)
;;
let rec tri_insertion = function
| [] -> []
| t::q -> insertion t (tri_insertion q)
;;Étude de la complexité de cet algorithme
Notons Ti(n) la complexité du tri par insertion d’une liste de taille n et I(n) la complexité de l’insertion d’un élément dans une liste de taille n. On a
Ti(n) = Ti(n-1) + I(n-1)
Ti(0) = 1
et dans le pire des cas,
I(n) = k + I(n-1)
I(0) = 1
On en déduit que I(n) = O(n) puis que Ti(n) = O(n²) dans le pire cas.
Dans le meilleur des cas, la liste est déjà trié, les insertions se feront en temps constant, on trouvera alors une complexité linéaire : Ti(n) = O(n)
En moyenne, la complexité est en O(n²).
Ce tri est efficace dans le cas où l’entrée est presque triée (comme le tri bulle), mais pas en moyenne. Pour améliorer la complexité, il faudrait diviser véritablement le problème, par exemple en coupant la liste en deux sous-liste.
Tri pivot
Le tri pivot contrairement au tri insertion ne va pas se contenter de réduire le problème d’une unité mais va tenter de fabriquer deux listes de taille moitié, d’appliquer récursivement l’algorithme de tri sur ces listes puis de réassembler les listes. Pour que le réassemblage soit facile, on choisit de prendre comme sous-listes une liste d’éléments inférieurs à un élément choisi que l’on nomme pivot et une liste d’éléments supérieurs à ce pivot. Le réassemblage consistera donc simplement à concaténer la première liste, le pivot puis la deuxième liste.
La partie plus compliquée de cet algorithme va être de constituer les deux listes en question. Le pivot va être choisi comme le premier élément de la liste.
Une fonction separe_aux pivot liste linf lsup va prendre une liste et retourner les listes linf et lsup composées respectivement des éléments inférieurs et des éléments supérieurs au pivot.
La fonction tri_pivot va donc, si la liste n’est pas vide va donc générer les listes linf, lsup = separe_aux pivot liste [] [], trier linf et lsup et les concaténer.
Exercice
- Implémenter la fonction
separe_aux. - Étudier la complexité de cette fonction.
- Implémenter la fonction
tri_pivot. - Étudier la complexité de cette fonction en supposant les sous listes de taille moitié de la liste de départ.
Tri fusion
Le tri fusion part du même constat que le tri pivot : il est plus intéressant de couper la liste en deux listes de même taille que de ne la réduire d’une unité. Cette fois, nous allons vraiment couper en deux listes “égales”, ce qui rendra le réassemblage (la fusion) plus complexe.
Exercice
- Implémenter la fonction
unzipqui prend une liste et fabrique d’une part la liste des éléments d’indice impair, d’autre part la liste des éléments d’indice pair. Le nom unzip vient de l’analogie avec une fermeture éclair : la liste initiale est la fermeture fermée, si on l’ouvre, on obtient d’un côté un élément sur deux, de l’autre côté les autres éléments. - Calculer la complexité de cette fonction.
- Implémenter la fonction
fusionqui prend deux listes triées et les fusionne en une seule liste triée. - Calculer la complexité de cette fonction.
- Écrire la fonction tri_fusion qui réalise le tri en “unzippant” la liste, triant chacune des sous-listes obtenues puis fusionnant les listes triées.
- Calculer la complexité de ce tri.
Tri par arbre
Nous pouvons utiliser les abr pour réaliser un tri par arbre. L’idée sera d’insérer tous les éléments de la liste dans un abr puis de faire le bon parcours d’arbre pour obtenir la liste des éléments triés.
- Implémenter le tri par arbre.
Références
- J.-P. Delahaye, P=NP, un problème à un million de dollars, http://interstices.info/jcms/c_21832/p-np-un-probleme-a-un-million-de-dollars, 2007
- X. Leroy, D. Doligez, A. Frisch, J. Garrigue, D. Rémy and J. Vouillon, The OCaml system, http://caml.inria.fr/pub/docs/manual-ocaml/index.html
- M. Sipser, Introduction to the Theory of Computation, PWS Publishing, 1997