The mploc software package
The mploc software package
Canonical lift
Using mploc, is is currently relatively easy to compute for instance
the canonical lift (Teichmüller lift) of a given definition polynomial up to arbitrary precision.
Let
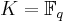 be a finite field. Consider an
unramified extension
be a finite field. Consider an
unramified extension
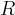 of
of
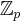 . A given
element
. A given
element
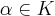 can be lifted to many different
elements. The canonical lift of
can be lifted to many different
elements. The canonical lift of
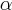 is the
unique element of
is the
unique element of
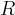 which maps to
which maps to
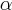 in the
residue field and which is at the same time a root of the
polynomial
in the
residue field and which is at the same time a root of the
polynomial
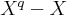 in
in
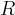 .
.
When the input data is an irreducible polynomial
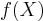 over
over
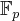 , consider an extension
, consider an extension
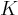 of
of
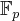 , and an unramified extension
, and an unramified extension
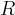 of
of
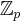 having
having
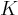 as a residue field. The
canonical lift of
as a residue field. The
canonical lift of
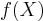 is the minimal polynomial of the
canonical lift of
is the minimal polynomial of the
canonical lift of
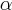 in
in
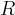 , where
, where
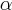 is a root of
is a root of
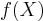 in
in
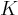 . The
canonical lift is defined over
. The
canonical lift is defined over
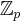 .
.
The mploc distribution contains code in the demo/
directory, more precisely files teich1.c and
teich2.c (see also the main calling code in
teich.c), which compute the canonical lift of a given
irreducible polynomial over
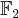 using various
algorithms.
using various
algorithms.
At present, the code in teich2.c in mploc-0.3
achieves the following
timings for lifting a polynomial of degree 163 up to the given precision.
Timings are in seconds on a 3.00GHz Intel Pentium 4 processor.
| precision | time |
| 256 | 0.04 |
| 512 | 0.08 |
| 1024 | 0.17 |
| 2048 | 0.36 |
| 4096 | 0.78 |
| 8192 | 1.73 |
| 16384 | 3.95 |
| 32768 | 7.72 |
| 65536 | 22.33 |